На прошлом уроке мы выяснили, что тела взаимно действуют друг на друга.
Также выяснили, что если на одну из одинаковых тележек поставить груз и пережечь нить, которая удерживает упругую пластину в согнутом состоянии, то тележка с грузом будет разгоняться медленнее. Это значит, что её инертность больше, чем инертность первой тележки.
Инертность – это свойство тела. У разных тел она разная. Это значит, что инертность можно выразить в количественном виде. Для этого существует физическая величина, под названием «масса».
Иначе говоря, масса – это мера инертности тела. Она обозначается латинской буквой m.
Тела могут взаимодействовать по-разному. Например, если натянуть между теми же тележками более тугую пружину, то они разлетятся в разные стороны с большими скоростями.
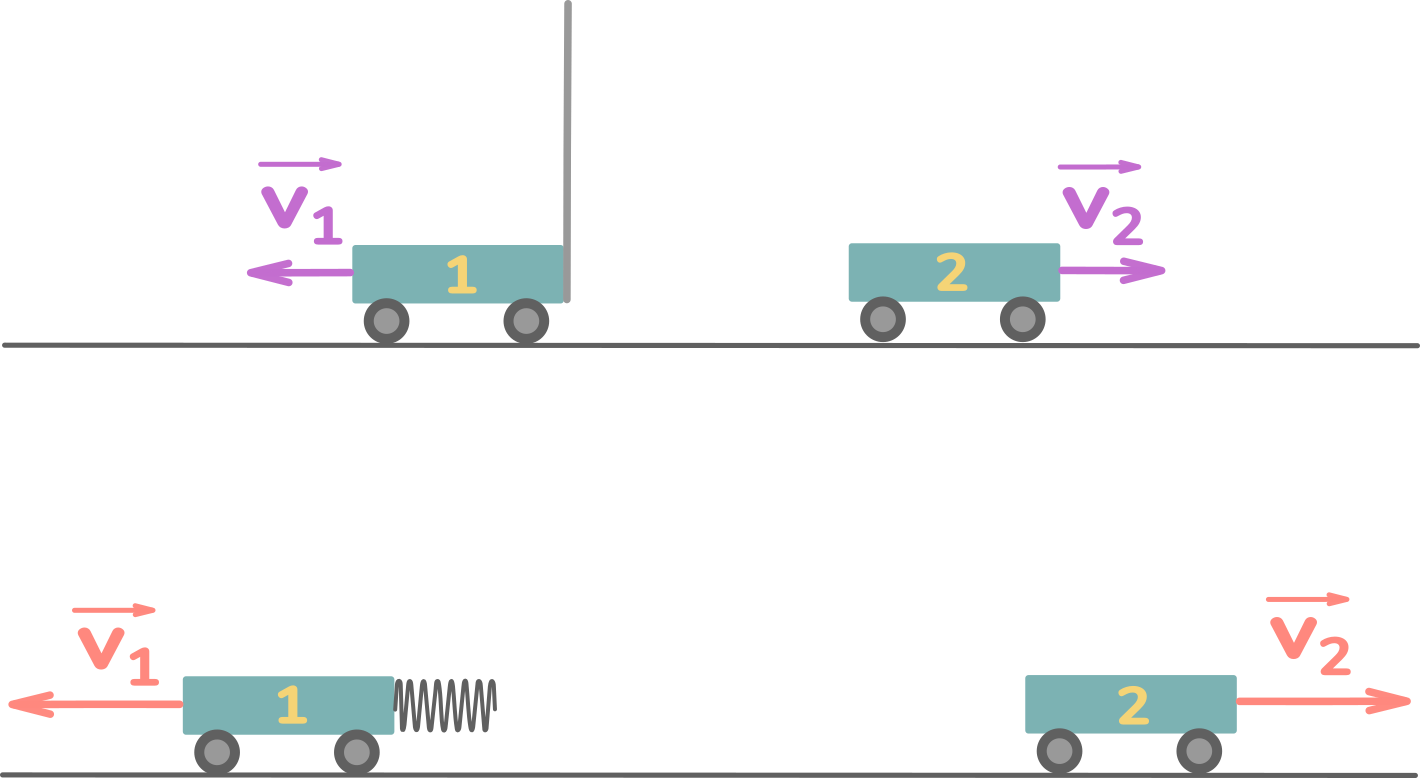
То есть v1 и v2 могут быть разными в зависимости от характера взаимодействия. Но для данных 2-х тел отношение v1 к v2 всегда одно и то же.
Следовательно, это отношение характеризует сами тела. Оно не зависит от того, каким образом они взаимодействовали друг с другом.
Мы знаем, что чем больше инертность тела, тем меньше его скорость.

Значит отношение v1 к v2 будет обратно пропорционально отношению инертностей первого и второго тела.
Так как мера инертности – это масса, то вместо слов инертность подставим знак массы, то есть латинскую букву m. Теперь наше уравнение выглядит так:
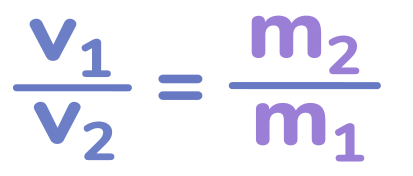
Из него видно, что мы можем сравнивать массы тел, сравнивая скорости, которые тела набрали после взаимодействия друг с другом.
Если мы хотим найти массу второго тела, то перепишем уравнение таким образом:
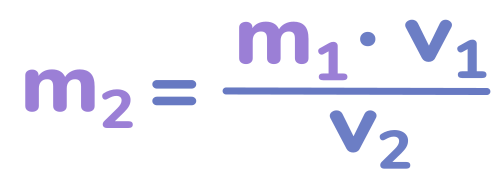
Теперь в качестве первого тела нужно взять тело известной нам массы, заставить его взаимодействовать со вторым телом, измерить скорости обоих тел после их взаимодействия и подставить получившиеся значения в эту формулу. Так мы узнаем массу второго тела.
За единицу массы в Международной системе единиц раньше была принята масса платиново-иридиевого цилиндра, хранящегося в городе Севре во Франции. Эта масса называется килограмм, сокращённо кг. Но сейчас есть более точный эталон массы, который выводится из фундаментальной физической константы под названием Постоянная Планка. В детали нового эталона вдаваться не будем.
С эталона массы изготавливаются копии, с них другие копии, с них следующие копии и так далее. Таким образом, если использовать копию эталона в качестве первого тела, то можно подставить его массу в наше уравнение. Так как масса эталона – единица, масса второго тела будет равна отношению скоростей обоих тел. Измерив их, мы узнаем массу второго тела.

Дальше при взаимодействии второго тела с третьим телом, мы сможем узнать массу третьего тела, так как масса второго тела нам уже будет известна. И так далее.
Помимо килограмма используются единицы, которые значительно больше или меньше него: тонна, грамм и миллиграмм.
1 тонна – это 1000 кг
1 г – это одна тысячная килограмма
1 миллиграмм – это одна миллионная килограмма.
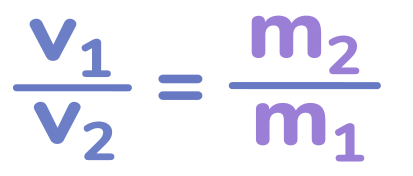
В этой формуле речь шла о модулях скорости. Но скорости – это векторы, то есть помимо величины они характеризуются ещё и направлением. А направления в нашем примере с тележками были противоположными. После взаимодействия, первая тележка направилась налево, а вторая направо.
Противоположное направление скоростей необходимо отобразить в нашей формуле.

Для этого проведём ось. Выберем положительное направление. Пусть оно будет вправо.
Тогда вторая тележка движется вдоль оси, и мы будем считать её скорость положительной, а первая движется против оси, и мы будем считать её скорость отрицательной. То есть v1 < 0, а v2 > 0. Если бы мы направили ось в противоположную сторону, то было бы наоборот.
Учитывая сказанное, перепишем нашу формулу. Так как одна из скоростей отрицательная, поставим перед левой дробью знак минус.
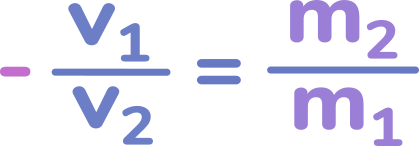
Эта формула уже учитывает направление скоростей.
Но она подходит только для тел, которые перед взаимодействием не двигались. В нашем случае тележки изначально были неподвижны.
Для тел, которые двигались ещё перед взаимодействием, нужна более точная формула. Ведь после взаимодействия скорости тел меняются. Соответственно наша формула должна отражать эти изменения.

Обозначим изменение скорости буквами Δv. Изменение скорости вычисляется как v конечная минус v начальная. Изменение может быть как положительным, так и отрицательным. Если скорость увеличилась, то изменение положительное, а если уменьшилась, то отрицательное.
Если тело изначально не двигалось, то v начальное равно нулю. Значит, из нашего уравнения v начальное можно вычеркивать. А дельта v, в таком случае, равна v конечной.
Теперь запишем окончательный вариант нашей формулы.
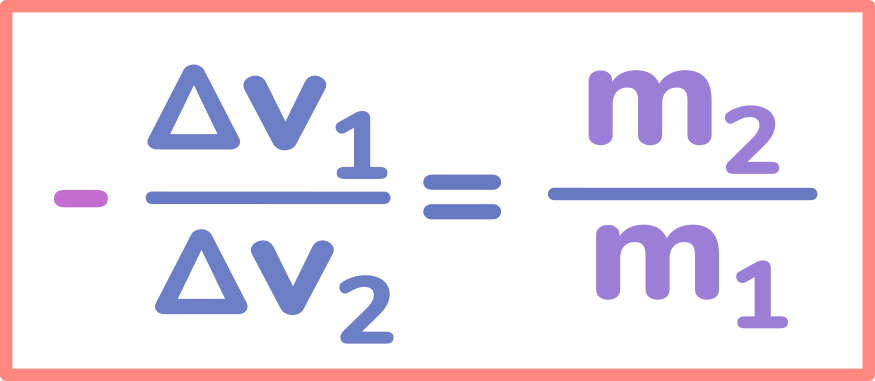
Её содержание звучит следующим образом. После взаимодействия двух тел, взятое со знаком минус отношение изменения скорости первого тела к изменению скорости второго тела равняется обратному отношению масс этих тел. Эта формула учитывает скорость движения тел до взаимодействия.