Сила упругости пружины возрастает во столько же раз, во сколько возрастает удлинение пружины.
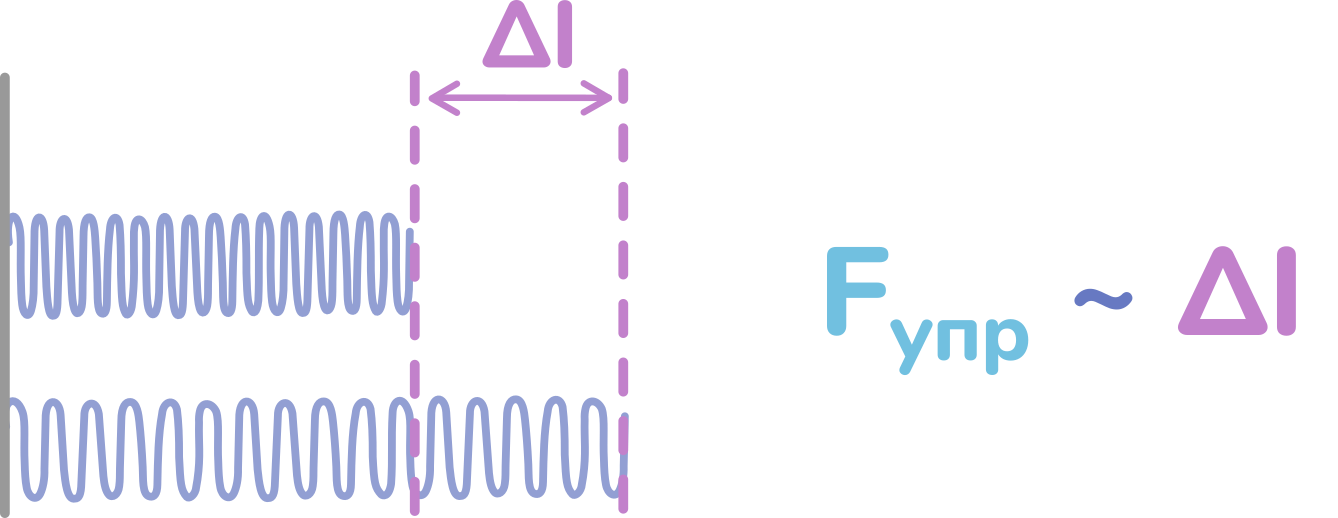
На этом основано устройство прибора для измерения силы – динамометра. Его название произошло от греческих слов динамис — «сила» и метрео – «измеряю».
Простой динанометр может быть устроен следующим образом: наверху пластины закреплён верх пружины на каком-нибудь выступающем стержне. В качестве стержня, например, может быть использован шуруп, ввинченный в пластину не до конца.
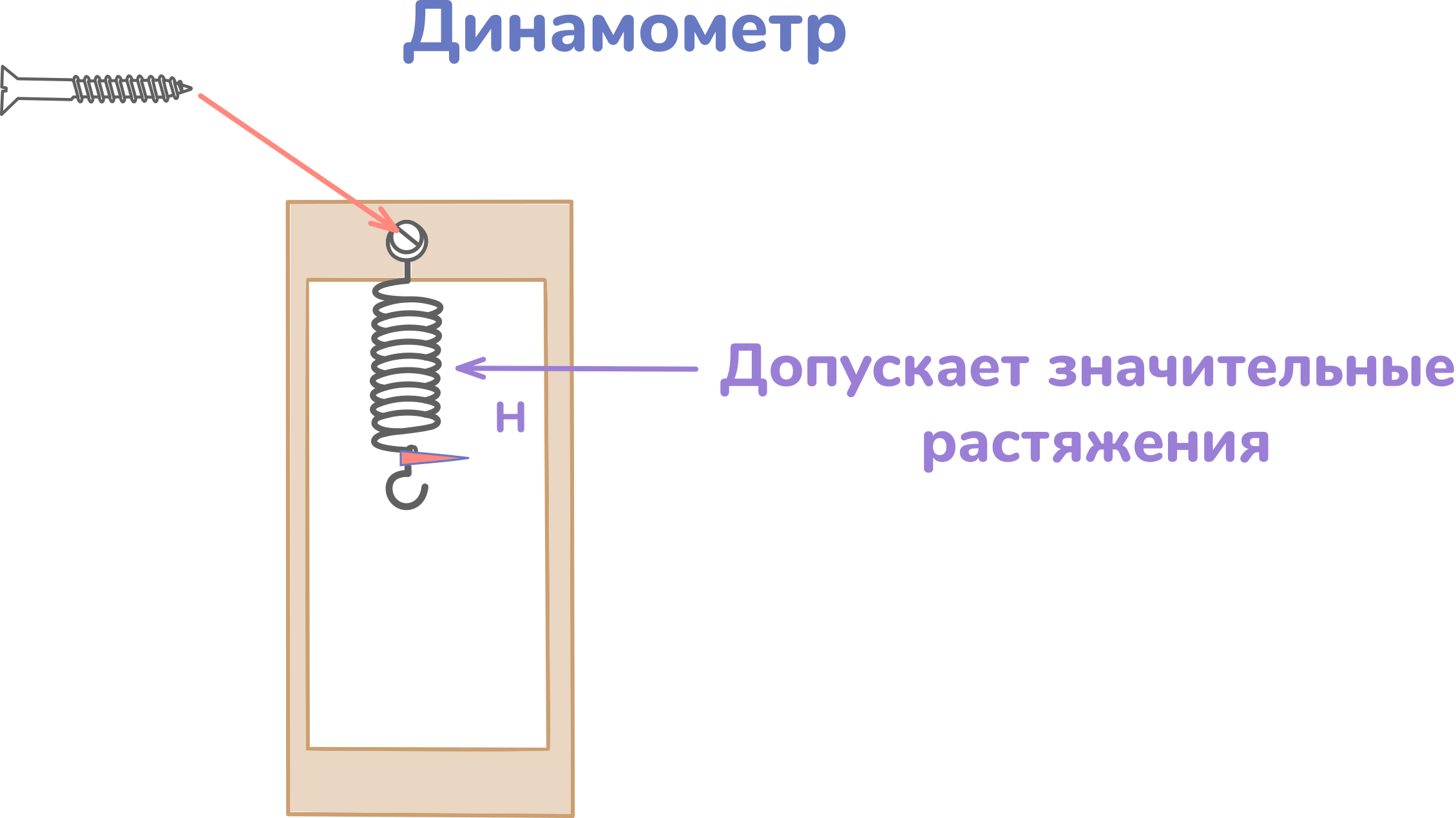
Пружина хороша тем, что допускает значительные растяжения. Так как витков много, деформация каждого из них будет маленькой. Благодаря этому закон Гука работает даже при больших растяжениях пружины.
На её нижнем конце подвешен крючок, на который можно вешать груз. Также на её нижнем конце закрепляется стрелка-указатель.
Дальше нужно проградуировать прибор, то есть нанести на него шкалу с делениями. Единицами измерения будут Ньютоны. Это нужно указать на приборе.
Отметим сначала нулевое деление. Оно соответствует положению указателя при нерастянутой пружине.
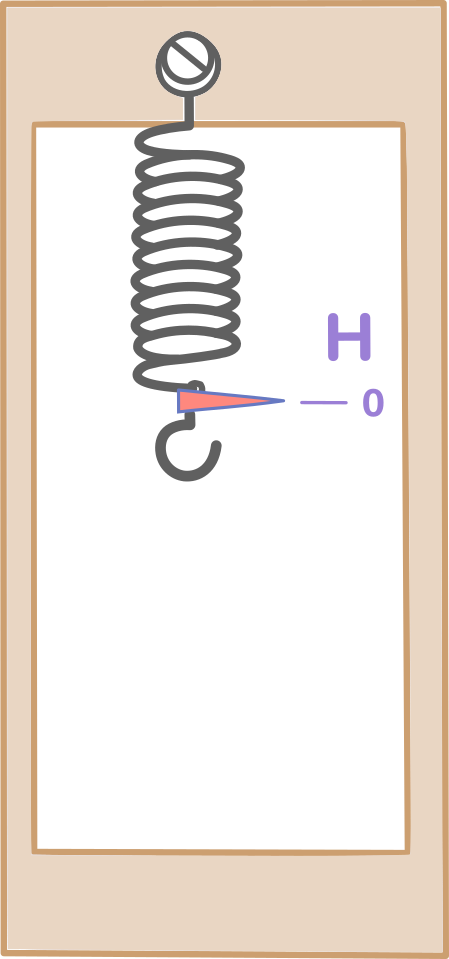
Затем на крючок подвешивается груз массой 1/9,8 кг. Дело в том, что на груз именно с такой массой действует сила 1 Н. 1/9,8 кг – это приблизительно 102 г.
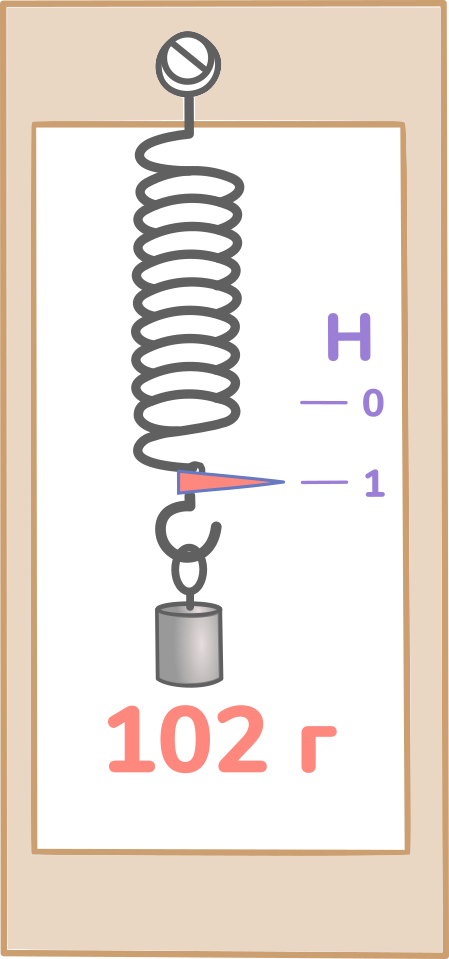
Под действием силы 1 Н пружина растягивается. Новое положение указателя отмечаем на пластине штрихом и ставим 1. То есть такое растяжение пружины соответствует силе в 1 Н.
Прикрепляем груз массой 204 г. Новое положение указателя будет соответствовать 2 Н.
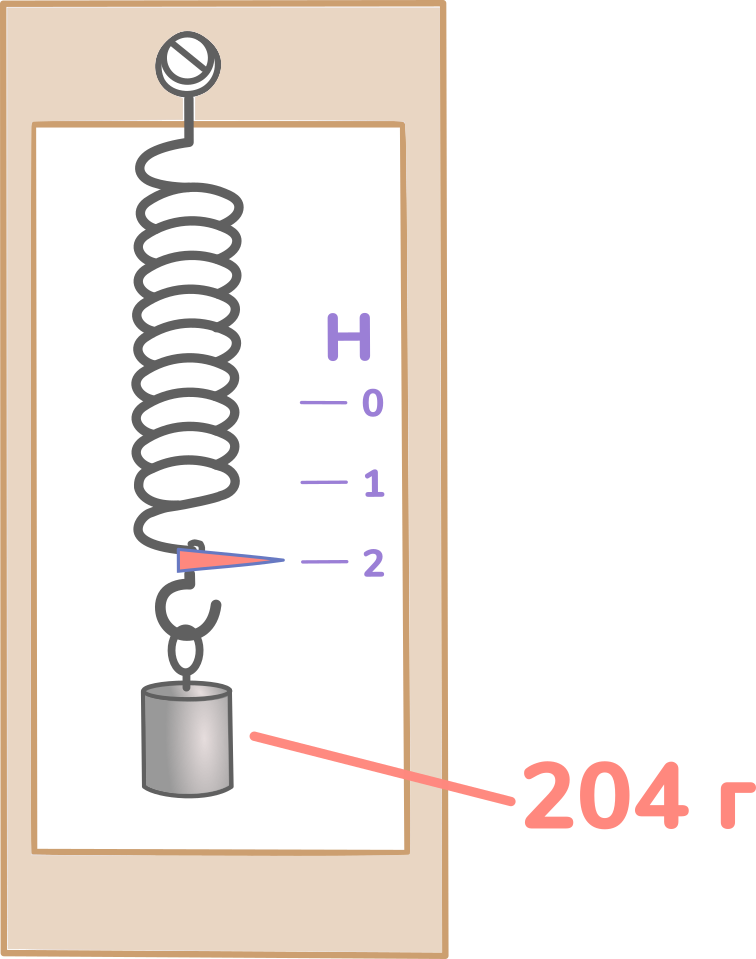
Дальше масса груза увеличивается каждый раз на 102 г, и наносятся штрихи, рядом с которыми числа будут больше предыдущих на 1. Это продолжается до тех пор, пока не доберёмся до значения, которое мы захотим сделать верхним пределом измерений. Пусть в нашем случае это будет 3 Н. Подвешиваем гирьку массой 306 г и узнаём, где поставить штрих, который соответствует 3 Н.

Затем каждый промежуток между штрихами можно разделить на другие равные промежутки. Давайте разделим на 5 равных промежутков. Мы получили деления, которые соответствуют 0,2 Н.
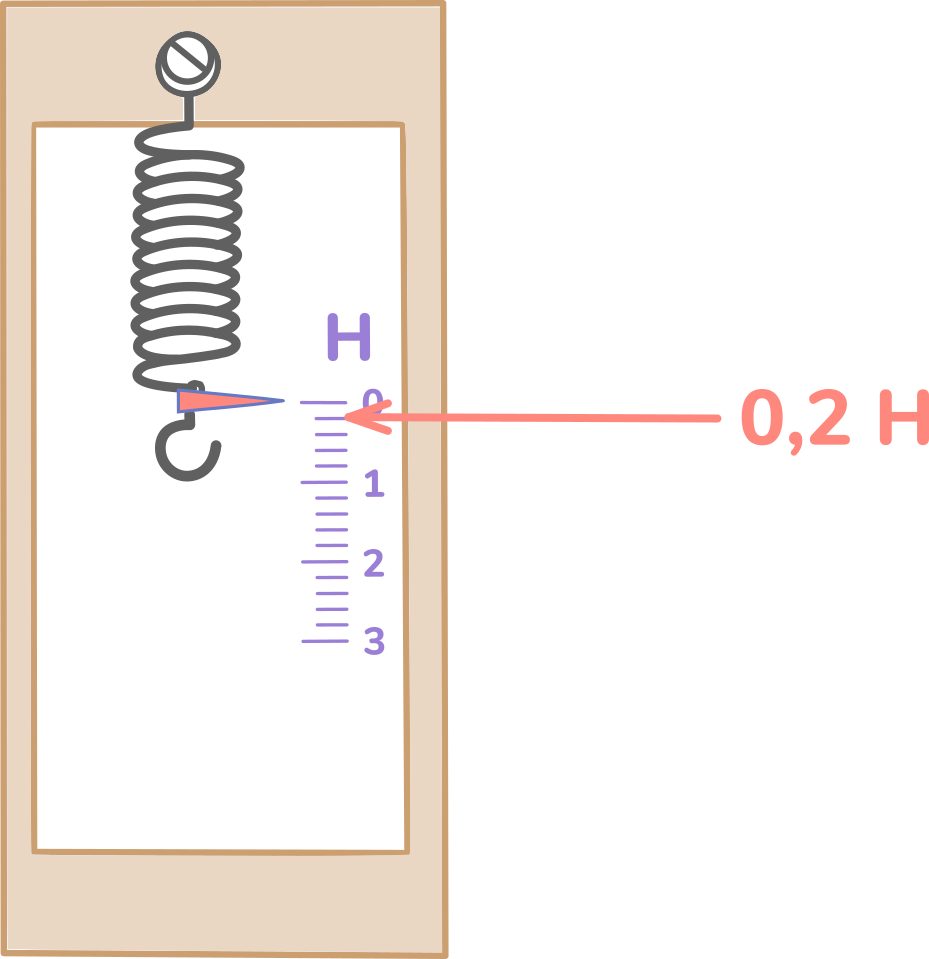
Простой динамометр готов. Его непосредственная задача в том, чтобы измерять разного рода силы, которые действуют на пружину.
Но если его проградуировать в единицах массы, то его можно использовать для измерения массы. Тогда динамометр можно назвать пружинными весами. Примером таких весов служит безмен, который используется там, где нет возможности использовать стационарные весы.

В предыдущих уроках мы знакомились с другим видом весов — с рычажными весами.
У них есть преимущество по сравнению с пружинными весами. Рычажные весы сравнивают силу, с которой гиря действует на чашку, и силу, с которой взвешиваемое тело действует на другую чашку. Если эти весы переместить на Луну, то они будут работать и там.

На Луне сила тяжести в 6 раз меньше, чем на Земле. Значит, во сколько раз уменьшится сила, с которой действует гиря на чашку, во столько же раз уменьшится сила, с которой действует взвешиваемое тело на другую чашку. Весы окажутся в равновесии, то есть покажут правильный результат.
А пружинные весы на Луне, покажут массу в 6 раз меньше реальной. То есть данные будут неверными.

Чтобы они работали на Луне, нужно учесть меньшую силу тяжести. Для этого нужно изменить их шкалу, то есть заново проградуировать.
На самом деле, если нужны сверхточные измерения на Земле, то у пружинных весов сохраняется этот же недостаток. Сила тяжести, которая действует на одну и ту же массу, в разных местах Земли немножко отличается.

Поэтому если на одних и тех же сверхточных пружинных весах взвешивать один и тот же предмет, например, на полюсе и экваторе, показания будут немножко отличаться.
Пружинные весы покажут точные результаты только в тех местах, где они проградуированы. То есть там, где составлена их шкала. В другом месте их нужно градуировать заново.