Перед вами 2 сосуда.

Они могут быть любой формы. В нижней части они сообщаются, то есть, соединены друг с другом трубкой.
На трубке установлен кран. Сейчас он закрыт. В первый сосуд нальём жидкость. Обозначим её плотность ρ1, а высоту столба жидкости h1. Во второй сосуд нальём жидкость с другой плотностью. Обозначим её ρ2, а высоту столба жидкости h2. Допустим, мы подобрали высоты столбов жидкости так, что при открытии крана, жидкости не будут перетекать из одного сосуда в другой. Иначе говоря, жидкости будут находиться в равновесии.
В этой точке давление обозначим p1, а в этой – p2. Исходя из того, что жидкости находятся в равновесии, p1 = p2.
Выразим давления через плотности жидкости и высоты столбов. По формуле гидростатического давления p = ρ·h·g.
Подставим в эту формулу значения в наших сосудах и получим p1 = ρ1·h1·g , а p2 = ρ2·h2·g. Так как по условию равновесия, давление в первом сосуде p1 равно давлению во втором сосуде p2, получается следующее равенство: ρ1·h1·g = ρ2·h2·g.
g сокращаются и у нас получается, что ρ1·h1 = ρ2·h2.
![]()
Это условие равновесия в разных жидкостях сообщающихся сосудов.
Исходя из условия равновесия, если плотность первой жидкости меньше, чем плотность второй жидкости, то высота первой жидкости должна быть больше, чем высота второй жидкости.
![]()
Теперь рассмотрим частный случай условия равновесия. Это случай, когда в сосудах находится одна и та же жидкость, иначе говоря, жидкость в них однородная.
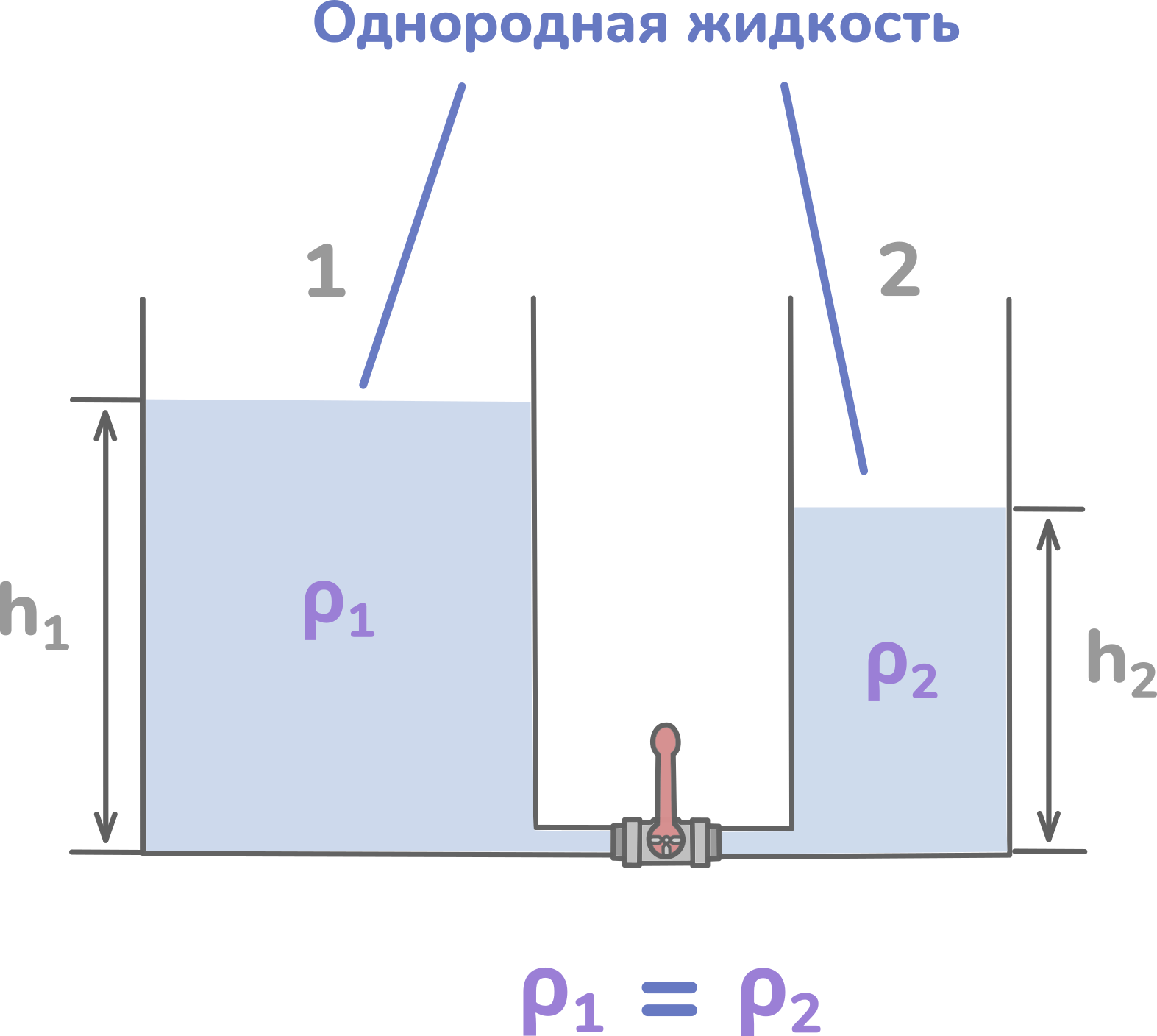
Это значит, что плотность жидкости в обоих сосудах одинакова, то есть ρ1 = ρ2. Так как плотность одна и та же, то можем её обозначить просто ρ, без всяких индексов.
Тогда можем переписать условие равновесия таким образом:
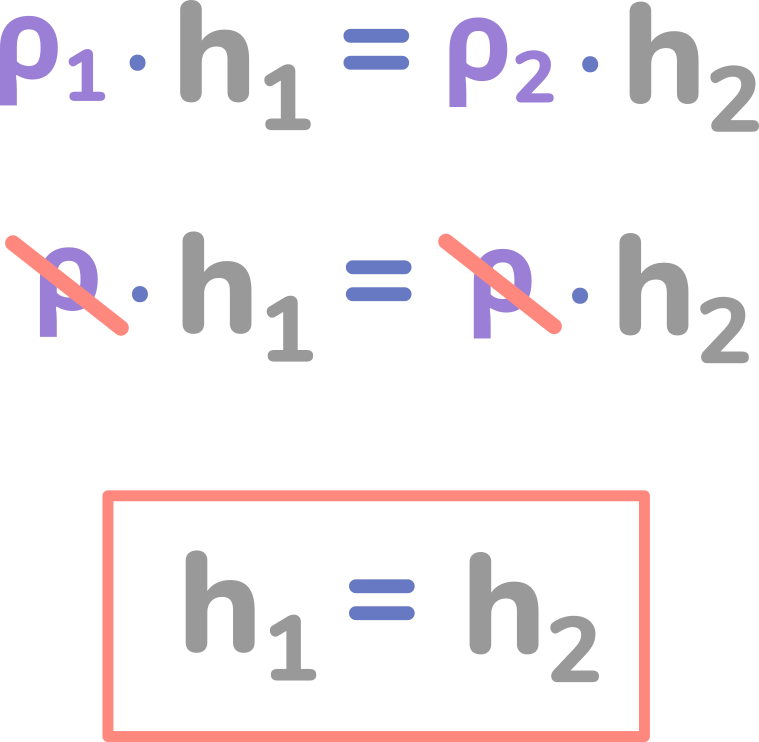
Если откроем кран, то убедимся, что h1 сравняется с h2.
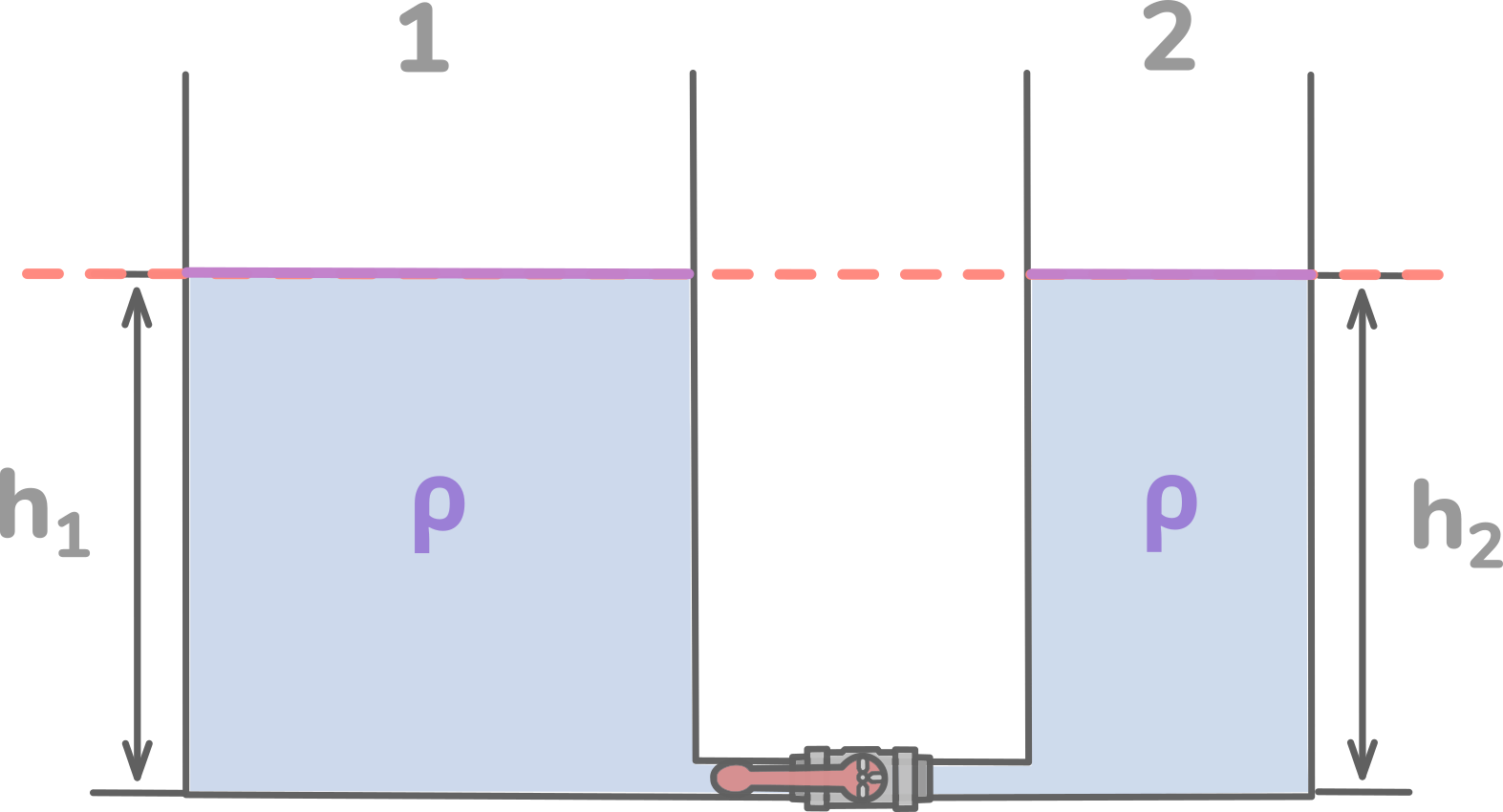
h1 = h2 — это математическое выражение закона сообщающихся сосудов.
А сам закон звучит следующим образом.
Свободные поверхности однородной покоящейся жидкости в сообщающихся сосудах любой формы, располагаются на одинаковой высоте.
Свободная поверхность – это поверхность жидкости, которая не соприкасается со стенками сосуда.
При этом сообщающихся сосудов может быть сколь угодно много, а форма у них может быть любой. Высота столба жидкости всё равно будет одинаковой.
