Примером простого механизма может служить домкрат.

Обычный человек не в состоянии приподнять часть автомобиля на высоту, необходимую для замены колеса. А с помощью домкрата это можно сделать без особых усилий. Ведь он позволяет, приложив меньшую силу в одном месте, получить большую силу в другом месте.
Некоторые другие простые механизмы наоборот позволяют, приложив большую силу, получить меньшую. Какие-то механизмы позволяют менять направление силы.
Таким образом, простыми механизмами называются устройства для преобразования силы.
Простые механизмы можно разделить на 2 класса:
- во-первых, это рычаг и его разновидности, а именно блок и ворот.
- а во-вторых наклонная плоскость и её разновидности: клин и винт.
В этом уроке остановимся на рычаге.
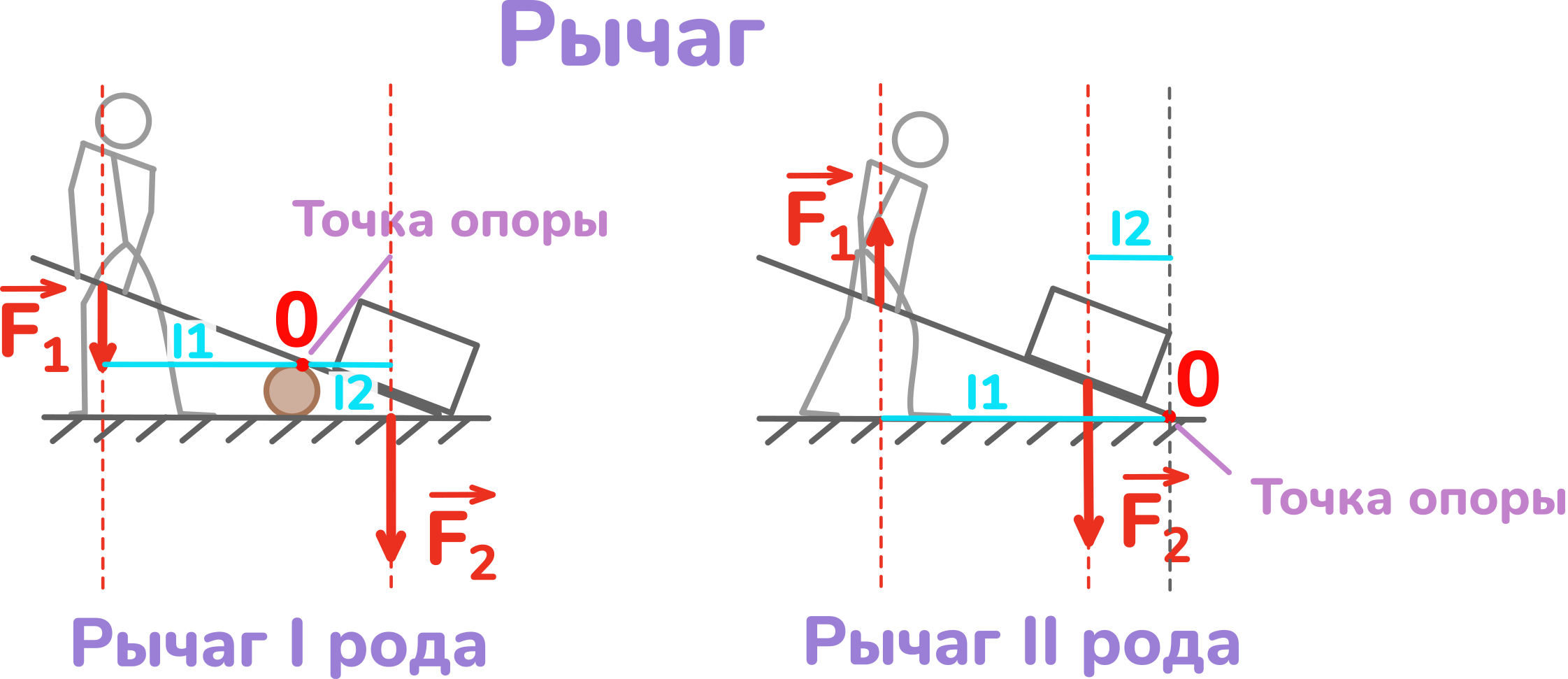
Перед вами груз, который нужно поднять. Для этого можно взять бревно и какое-то твёрдое тело, например лом. Подсовываем его под груз и, подкатываем бревно, и, опираясь на него, давим вниз на противоположный конец с силой F1. Вес груза обозначим F2. Лом в данном случае – это и есть рычаг. Место, где рычаг касается бревна, называется точкой опоры. Точка опоры неподвижна. Обозначим её буквой О.
Такой рычаг называется рычаг первого рода.
В рычаге второго рода обходятся без бревна. Он также подсовывается под груз, но давить на противоположный конец нужно не вниз, а вверх. Точка опоры в этом случае будет здесь.
В обоих вариантах рычаг – это твёрдое тело, которое вращается вокруг точки опоры. Отсюда определение. Рычаг – это твёрдое тело, способное вращаться вокруг неподвижной оси.
В описание рычага также входит физическая величина под названием плечо силы.
Найдём плечи силы в наших примерах. Для этого отметим линию действия силы F1. Затем отметим кратчайшие расстояния от линии действия силы до оси вращения. Это и есть плечо силы F1. Обозначим его l1.
Теперь проведём линию вдоль действия силы F2. Проведём перпендикуляр из точки О к этой линии. Это будет плечо силы F2. Назовём его l2.
С рычагом второго рода поступим также. Проводим линии действия сил. Перпендикуляр к точке опоры от линии действия силы F1 – это плечо l1, а перпендикуляр от линии действия силы F2 – это l2. И первое, и второе плечо оказываются на одной линии, поэтому второе плечо на рисунке сместим параллельно первому для наглядности.
Отсюда следует следующее определение. Плечом силы, относительно некоторой оси, называется кратчайшее расстояние от линии действия силы до этой оси.
Перед вами рычаг первого рода.
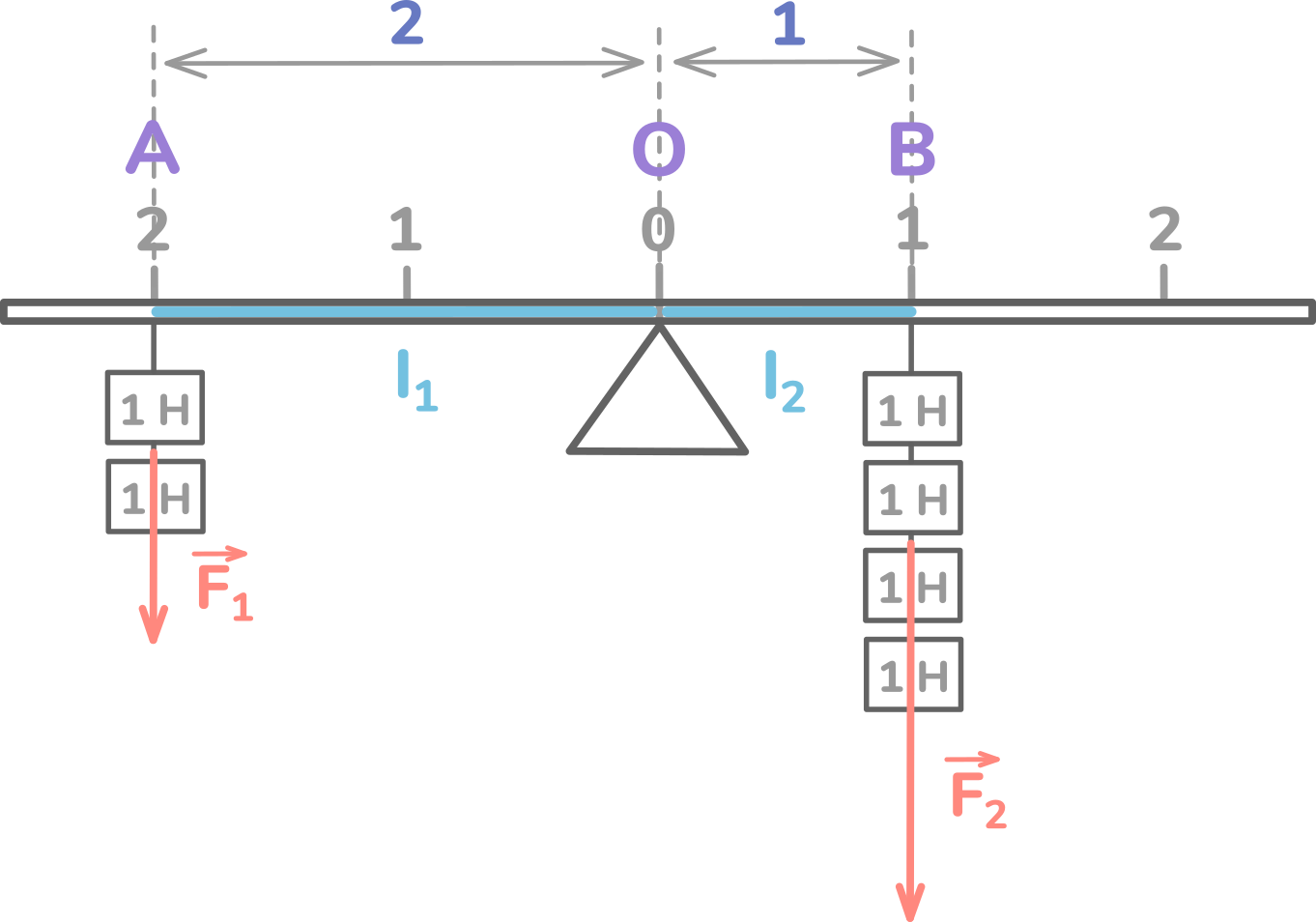
На нём с обеих сторон от опоры подвешены гирьки по 1 ньютону каждая. ОА – это плечо силы F1, а OB – плечо силы F2.
Количество гирек разное, но рычаг находится в равновесии. Дело в том, что равновесие зависит не только от модуля сил F1 и F2 и их направления, но и от точек их приложения.
Сила F1 складывается из веса двух гирек и получается 2 ньютона. Сила F2 складывается из 4-х гирек, поэтому получается 4 ньютона. При этом плечо силы F1 в 2 раза больше плеча силы F2.
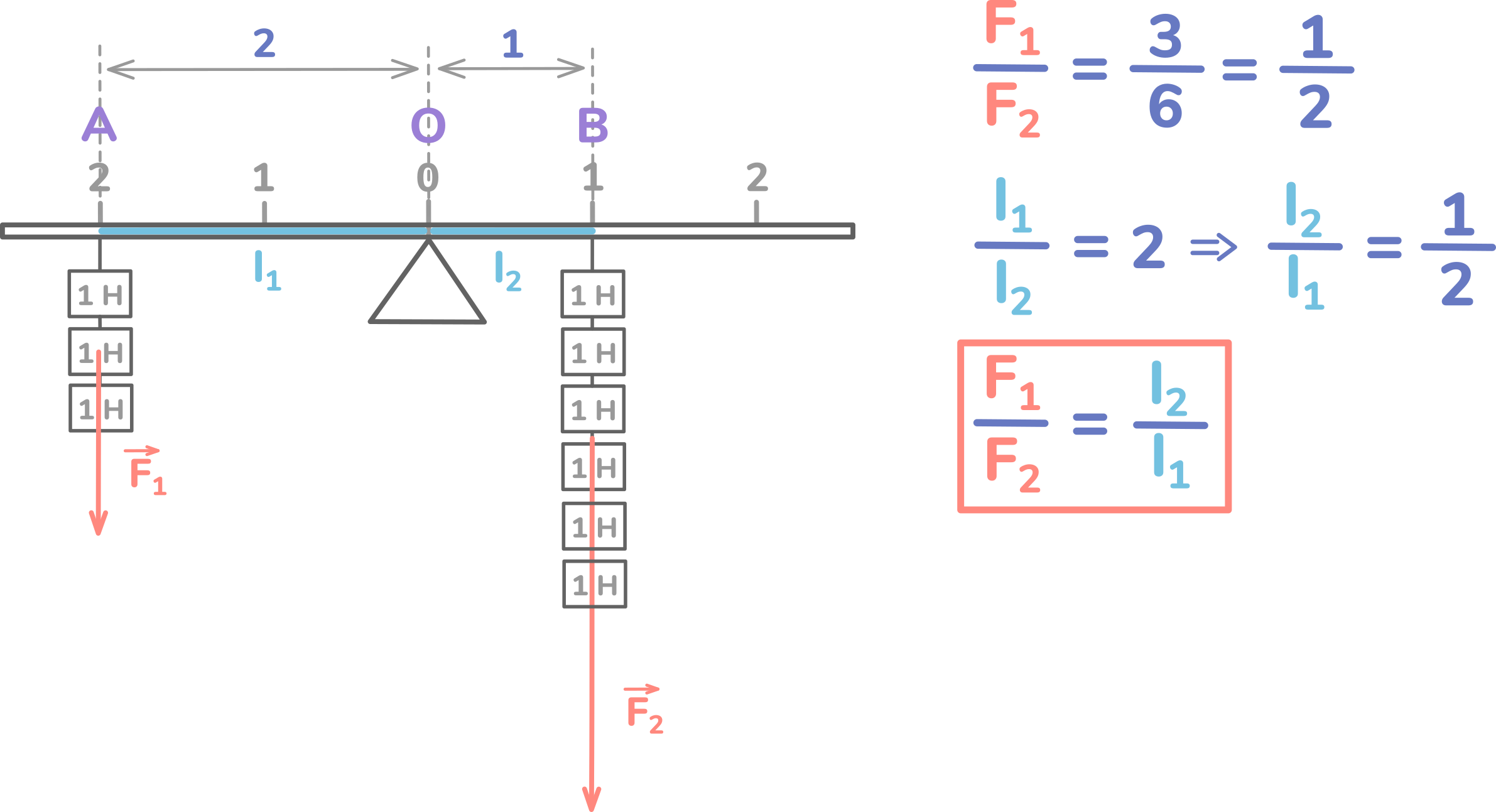
Если добавить 1 гирьку налево и 2 гирьки направо, то рычаг останется в равновесии.
Найдём отношение F1 к F2. В этом случае, это 3 к 6, то есть 1/2.
Также найдём отношение плеча l1 к l2. Оно оказывается равным 2. Это значит, что отношение плеча l2 к l1 равно 1/2.
Получается отношения сил F1 и F2 равно обратному отношению плеч l2 и l1.
Если переставлять точки приложения сил вдоль рычага и подвешивать разные грузы, это уравнение остаётся верным. Это и есть условие равновесия рычага.
Словами это условие выражается следующим образом. Рычаг находится в равновесии если отношение приложенных к нему двух сил равно обратному отношению плеч этих сил.
Исходя из условия равновесия, F1 = F2· l2/l1. Если увеличивать l1, то F1 уменьшается. Получается с помощью увеличения длины рычага можно получить выигрыш в силе.
Допустим нужно поднять груз, вес которого равен F2.

Тогда чем дальше от точки опоры сила, прилагаемая для подъёма груза, тем меньше она должна быть. Иначе говоря, чем длиннее плечо l1, тем легче поднять груз.
Отношение F2 к F1 называется выигрыш в силе.
Выиграть в силе можно очень много. Но чем больше выигрыш в силе, тем больше проигрыш в длине плеча.