Перед вами рычаг и условие его равновесия.
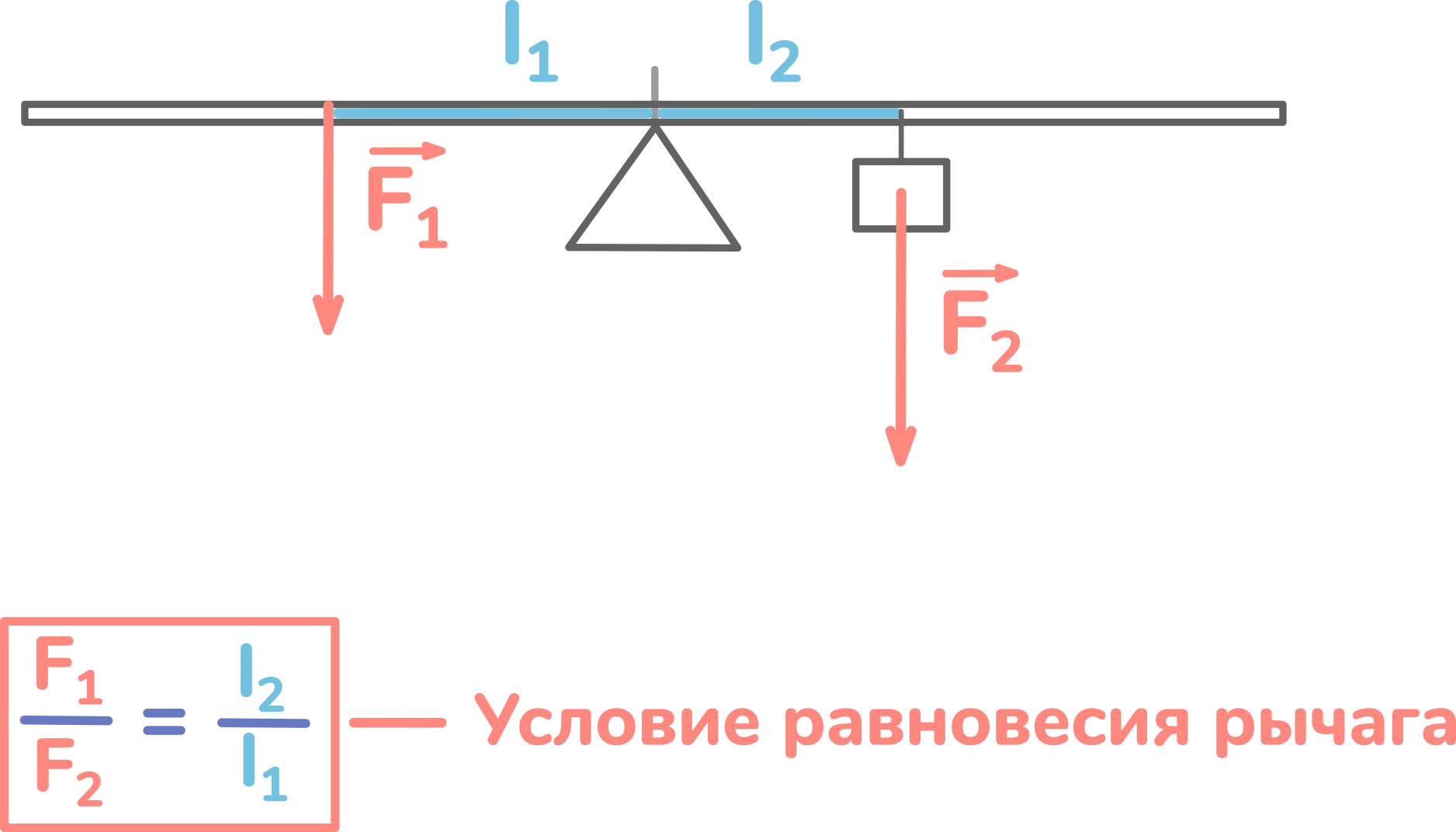
Это условие имеет ограниченные возможности. Оно подразумевает, что на рычаг действует всего 2 силы.
Чтобы находить условие равновесия для любого количества сил, действующих на рычаг, применяется физическая величина под названием момент силы.

По свойству пропорции, условие равновесия можно переписать следующим образом: F1·l1 = F2·l2.
Теперь слева стоит произведение модуля первой силы на своё плечо, а справа произведение модуля второй силы на своё плечо.
Получается, если эти произведения одинаковы, то рычаг в равновесии, а если не одинаковы, то он не в равновесии.
Каждое из этих произведений называется моментом силы.
В общем виде, момент силы обозначается буквой М и равен произведению модуля силы F на своё плечо l.
Его определение следующее. Моментом силы относительно некоторой оси называется физическая величина, равная произведению модуля силы на плечо силы относительно этой оси.
В нашем случае, момент силы M1 = F1·l1, а момент силы M2 = F2·l2.
Определим единицы измерения момента силы.
Из формулы получается, что его единица — это ньютон, умноженный на метр. Её так и называю ньютон-метр.
Если подставить момент силы в условие равновесия, оно будет выглядеть следующим образом: М1 = М2
Теперь рассмотрим случай, когда на рычаг действует больше 2-х сил.

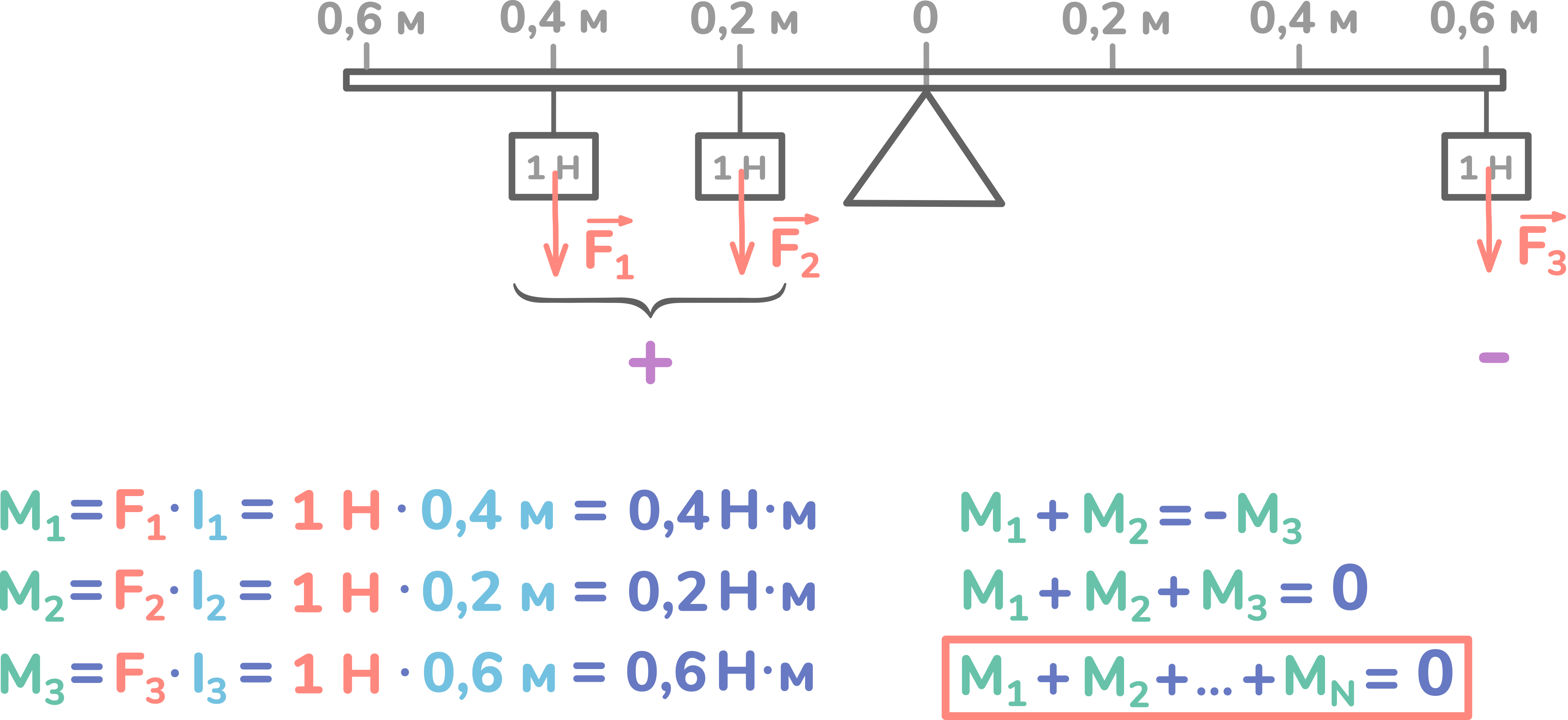
На этот рычаг слева от опоры подвешены гирьки в двух местах, а справа в одном месте. Вес каждой гирьки 1 Н.
Получается, на рычаг действует 3 силы и при этом он находится в равновесии.
Найдём моменты для каждой силы, перемножив силы на свои плечи.
M1 получится равен 0,4 Н м, M2 = 0,2 Н м, а М3 = 0,6 Н м.
Первый и второй моменты вращают рычаг против часовой стрелки, а третий момент — по часовой.
Чтобы не путать, какие моменты в каких направлениях вращают рычаг в их индексы добавляют «по» и «против».
Если сложить M1 и M2, то есть все моменты, вращающие рычаг против часовой стрелки, то их сумма будет равна величине третьего момента, то есть момента вращающего рычаг по часовой стрелке.
Получается условие равновесия для нашего случая с тремя силами следующее: M1против + M2против = M3по.
Но если проделывать опыты с большим количеством сил, то результат будет таким же.
Условие равновесия в таком случае формулируется следующим образом. Рычаг находится в равновесии, если сумма моментов сил, вращающих его по часовой стрелке равна сумме моментов сил, вращающих его против часовой стрелки.
Это условие называется правилом моментов.
Чтобы каждый раз не писать в индексах по и против, гораздо удобнее использовать разные знаки.
Если направление против часовой стрелки выбрать в качестве положительного, то вращение по часовой стрелки будет отрицательным.
В нашем случае M1 и M2 окажутся положительными, а M3 отрицательным.
Отсюда получается, что сумма этих моментов равна нулю.
Тогда правило моментов будет выглядеть таким образом: M1+M2+Mn = 0.
Формулируется оно следующим образом. Рычаг находится в равновесии, если алгебраическая сумма моментов сил, действующих на него, равна нулю.
Алгебраическая сумма учитывает знаки слагаемых.