Вычисление площади фигур вам должно быть известно из уроков математики. Но, на всякий случай, основные моменты стоит повторить. Они понадобятся для решения задач по физике.
Начнём с самой простой фигуры – с квадрата.

Обозначим его площадь большой буквой S от английского слова Square. А его сторону обозначим буквой а.
Для вычисления площади, нужно длину одной его стороны умножить на длину другой стороны. У квадрата все стороны равны, значит умножается а на а. По другому, это можно записать как а во второй степени.
Теперь вычислим площадь любого прямоугольника.
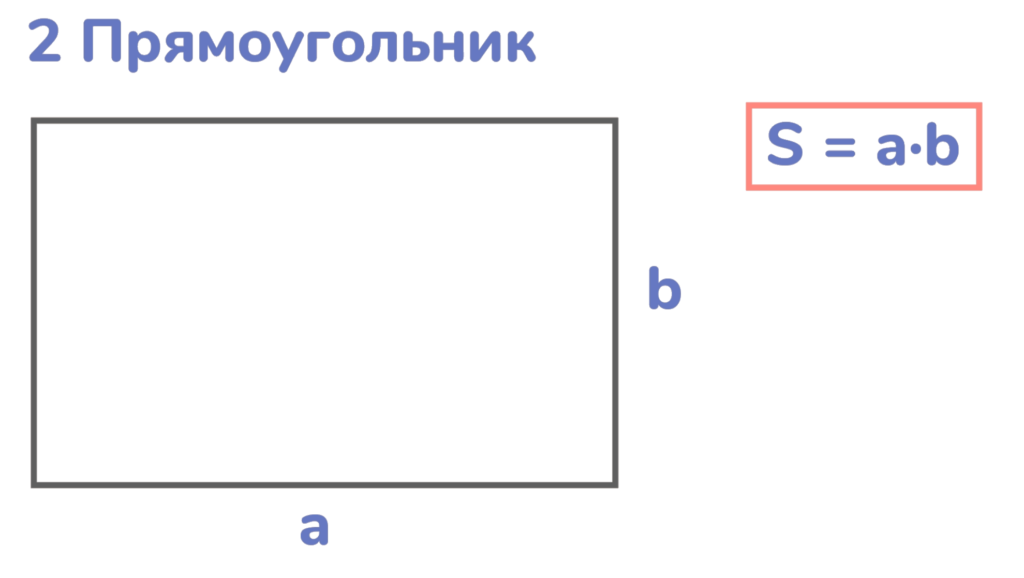
Длину одной стороны обозначим буквой а, длину другой стороны — буквой b. Площадь прямоугольника равна: а · b.
Теперь вычислим площадь любого треугольника.

Обозначим площадь треугольника Sт. Его основание обозначим буквой a. Проведём в треугольнике следующую линию. Она называется высота. Обозначим её буквой h.
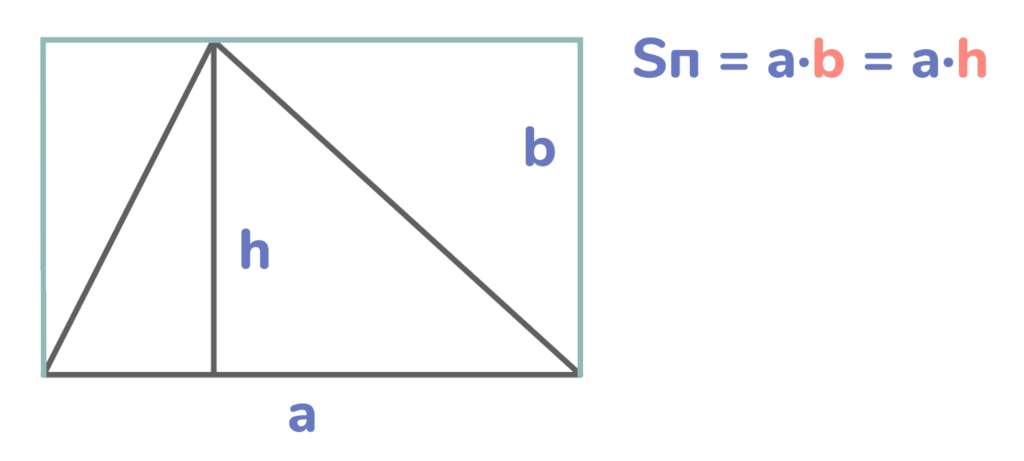
Площадь треугольника – это 1/2 от произведения его основания на высоту.
Теперь перейдём к вычислению площади круга.

Круг можно описать всего лишь одним числом – радиусом или диаметром. Обозначим радиус как r, а диаметр как d.
Диаметр в 2 раза больше радиуса. Соответственно радиус – это половина диаметра.
Длину окружности обозначим буквой l.
Какого бы диаметра ни была окружность, отношение длины окружности к её диаметру всегда одно и то же и равно 3 целых, а дальше бесконечное число цифр после запятой: 3,1415926535… Но так как, в нашем случае, высокая точность не важна, ограничимся 2-мя цифрами после запятой. Получается отношение длины любой окружности к её диаметру приблизительно равно 3,14.
Это число обозначается греческой буквой π, так как впервые его ввёл в употребление Пифагор.
Число π входит в формулу площади круга. Вот она: S= π·r².
Площадь также можно вычислить используя диаметр вместо радиуса. Получится π · (d/2)², что можно переписать как π·d²/4.
Эти 2 формулы понадобятся в дальнейшем для решения задач.
Теперь перейдём к площадям фигур неправильной формы. В этом случае речь пойдёт не об их вычислениях, а об их измерениях.
Используем для этого метод палетки. Палетка – это сетка. Допустим у нас такая фигура.

Крестиками зарисуем клетки, которые полностью находятся внутри этой фигуры. Точками отметим клетки, которые не целиком закрываются фигурой.
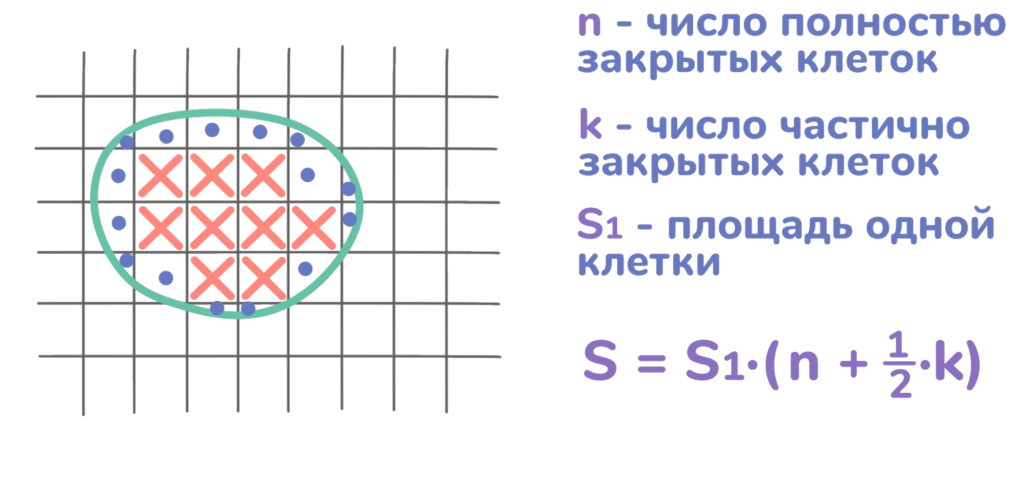
Пусть n – число полностью закрытых клеток, k– число частично закрытых клеток, S1 — площадь одной клетки.
Если площадь одной клетки умножать на n, это будет площадь фигуры, которую образуют полностью заполненные клетки.
А площадь одной клетки умножить на одну вторую ка даст нам площадь фигуры, которую образуют частично заполненные клетки.
Мы используем одну вторую, потому что, в среднем, частично заполненные клетки заполнены на половину, поэтому их площадь в два раза меньше, чем была бы при полностью закрашенных клетках. Разумеется, точность такого метода измерения имеет ограничения (как и точность любого метода измерения).
Вся площадь фигуры S вычисляется по формуле, представленной на рисунке.