Перед вами гидравлическая машина.

Она состоит из 2-х сообщающихся сосудов с разными площадями поперечного сечения. Внутри располагается жидкость и по поршню в каждом цилиндре.
При перемещении малого поршня на расстояние h1, большой поршень перемещается на расстояние h2. Для перемещения, к малому поршню прикладывается сила F1, а большой поршень действует на прессуемое или поднимаемое тело с силой F2.
Было установлено, что во сколько раз сила F2 больше, чем сила F1, во столько раз расстояние h1 больше расстояния h2. Получается во сколько раз выигрыш в силе, во столько же раз получается проигрыш в расстоянии, на которое перемещается поршень.
Эта закономерность имеет общий характер. Она применима и к любым вариантам рычага.
Перед вами рычаг.
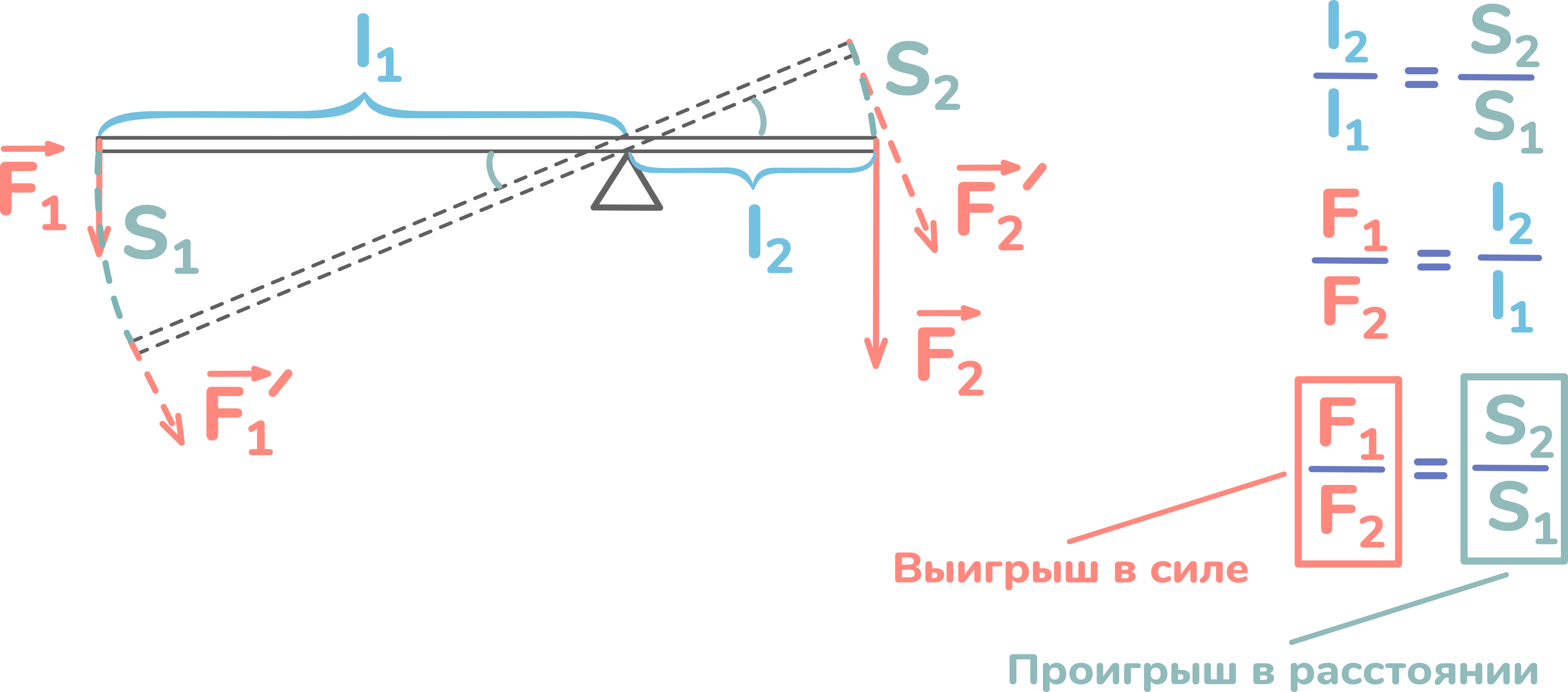
Отметим силы и плечи. Повернём его вокруг точки опоры. Отметим новые положения сил и плеч.
Отметим расстояния, пройденные точками приложения сил. Точка, к которой приложена сила F1 прошла расстояние S1. А точка, к которой приложена сила F2 прошла расстояние S2.
Во сколько раз l2 меньше, чем l1, во столько же раз S2 меньше, чем S1.
Получается такое соотношение: l2/l1 = S2/S1.
Запишем условия равновесия рычага: F1/F2 = l2/l1.
Исходя из первого отношения, заменим l2/l1 на S2/S1.
Получится F1/F2 = S2/S1.
F1/F2 показывает во сколько раз сила F1 меньше силы F2. А S2/S1 показывает во сколько раз расстояние S2 меньше расстояния S1.
То есть первое — это выигрыш в силе, а второе — это проигрыш в расстоянии.
Это математическое выражение золотого правила механики:

А формулируется оно следующим образом. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии.
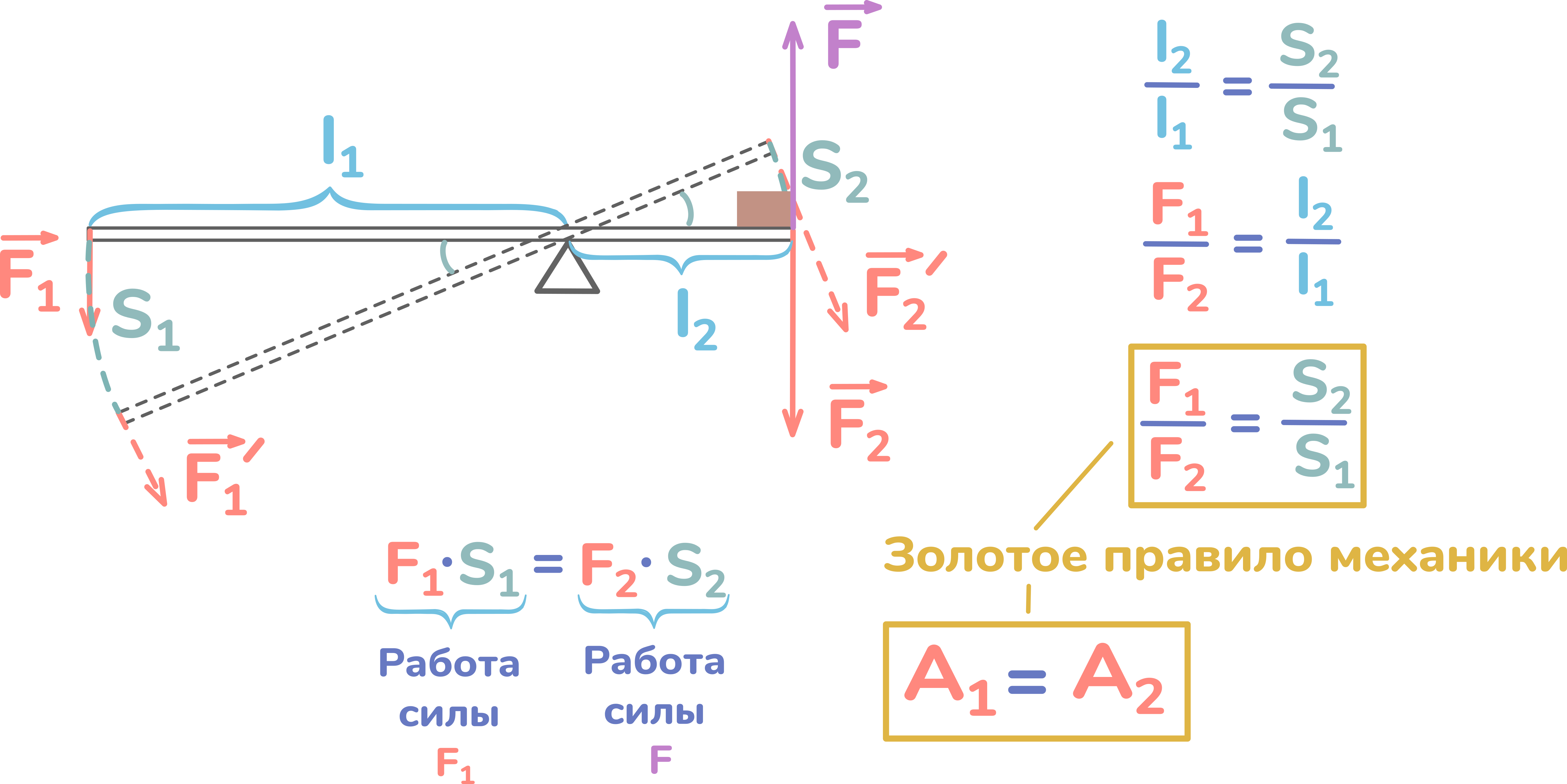
Воспользовавшись правилом пропорции, получим следующее равенство: F1·S1 = F2·S2.
В реальной ситуации, с правой стороны расположен груз, который действует на рычаг с силой F2. Для его равномерного поднятия, к нему должна быть приложена сила F, равная по модулю F2, но направленная в противоположную сторону.
Исходя из определения механической работы, левый член уравнения является работой силы F1, а правый — работой силы F.
Отсюда получается такая формула: А1 = А2.
Это также является золотым правилом механики, но выраженным через работу. Формулируется оно следующим образом. Работа по приведению простого механизма в действие, равна работе, совершаемой этим механизмом.
Золотое правило механики подразумевает отсутствие сил трения и невесомость деталей механизма. Так как в реальном мире присутствуют как силы трения, так и вес деталей, то прикладываемая работа оказывается больше работы, совершаемой механизмом.
Касаемо выигрыша в силе, он оказывается меньше, чем проигрыш в расстоянии.
В связи с этим справедлива более строгая формулировка золотого правила механики. Выигрыш в силе, при использовании простых механизмов, не превышает проигрыш в расстоянии.