Абсолютно точных измерений не бывает. Точность – понятие относительное. Одними приборами мы можем что-то измерить с меньшей точностью, а другими с большей точностью.
Давайте посмотрим, чем отличаются приборы с разной точностью.
Перед вами монета. Измерим её диаметр.
Сначала измерим мерной лентой.
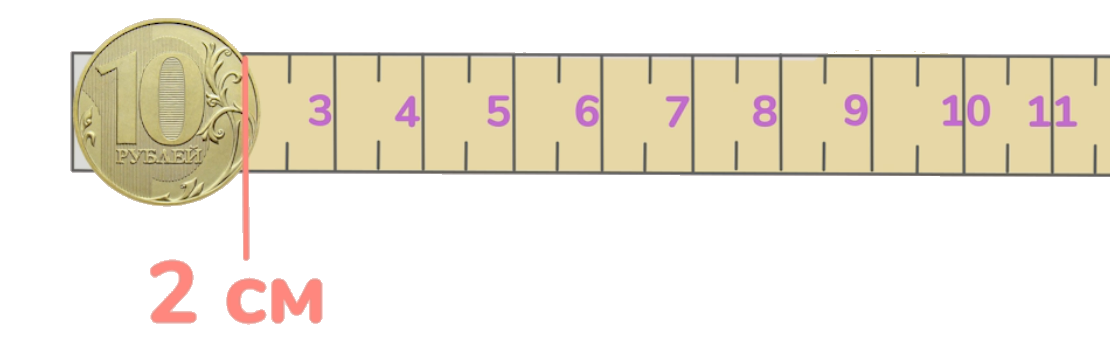
Один край монеты размещаем на нулевом штрихе. И смотрим, где оказался её противоположный край. Он оказался ближе к штриху, который отображает 2 см. Исходя из этого, можно сказать, что диаметр равен 2 см. Точность измерения принято считать равной половине цены деления. Цена деления мерной ленты 5 мм, иначе говоря, полсантиметра. Значит, реальный диаметр находится в диапазоне от 1,75 см до 2,25 см.
Теперь возьмём школьную линейку.
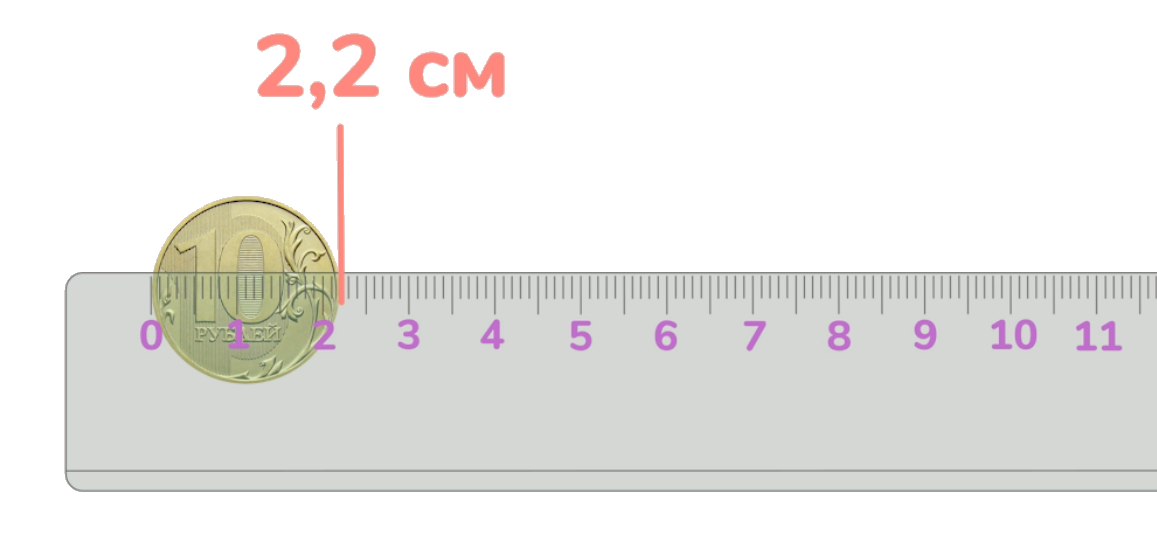
Мы видим, что диаметр не 2 см, а 2,2 см. Точность в данном случае полмиллиметра, иначе говоря, 0,05 см. Значит реальный диаметр находится в промежутке от 2,15 см до 2,25 см.
Дальше возьмём штангенциркуль.

Посмотрим, что показывает нониус. Его нулевой штрих оказался правее 2,1 см и чуть-чуть левее 2,2 см. А 9-й штрих совпадает с делением основной шкалы. Значит диаметр монеты 2,19 см. Но так как точность данного штангенциркуля 0,1 мм, иначе говоря, 0,01 см, реальный диаметр находится в диапазоне от 2,18 см до 2,20 см.
Теперь используем микрометр.

На нём есть основная шкала. У неё цена деления 1 мм. Также есть промежуточная основная шкала. Она смещена на полмиллиметра. Если край цилиндра приходится не на основную шкалу, а на промежуточную основную шкалу, то нужно прибавить полмиллиметра. Микрометрическая шкала расположена на барабане, который при вращении смещается влево, либо вправо относительно основной шкалы. Это сопровождается изменением расстояния между мерительными поверхностями. Между ними помещается монета и зажимается. У микрометрической шкалы цена деления 0,01 мм.
В нашем случае, основная шкала показывает 21 мм. Но край барабана расположен правее отмеченного фиолетовым цветом штриха промежуточной основной шкалы. Значит к 21 мм прибавляем ещё полмиллиметра. Микрометрическая шкала показывает 44 сотых миллиметра. Прибавляем их к предыдущему результату и получаем 21,94 мм, иначе говоря 2,194 см. Точность данного микрометра 0,01 мм, иначе говоря 0,001 см, значит реальный диаметр находится в диапазоне от 2,193 см до 2,195 см
Обратите внимание: чем точнее измерение, тем больше цифр в результате. Для того, чтобы охарактеризовать точность измерения, используется понятие «значащие цифры».
Давайте возьмём наше последнее число и запишем его в миллиметрах, сантиметрах, дециметрах и метрах.

Оно записано по-разному, но везде осталось одинаковое количество значащих цифр, а именно 4.
Количество значащих цифр определяет точность, с которой мы отображаем результат измерения.
Первые цифры называются верные знаки, а последняя цифра называется сомнительная цифра. Сомнительная, потому что она может оказаться любой другой из диапазона возможных значений, определяемого точностью измерительного прибора.
Из показанных здесь вариантов записи одного и того же числа видно, что количество знаков после запятой к точности не имеет отношения. Всегда нужно смотреть на цифры, расположенные справа.
Если, после запятой, справа стоят нули, то они являются частью значащих цифр и указывают на точность.
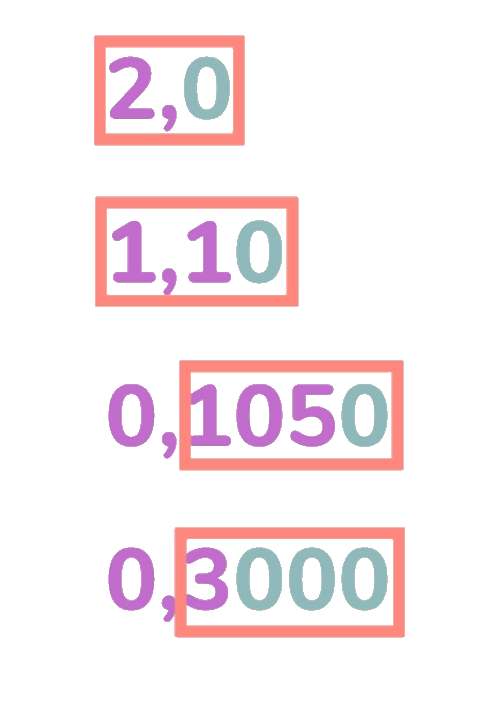
Напоследок отмечу, что не стоит всегда стремиться к наибольшей точности. Точность должна быть достаточной для решения конкретной задачи.
Чтобы это лучше усвоить, представьте иголку. Она не должна быть идеально острой. Она должна быть достаточно острой, чтобы шить.